vtkCookieCutter: Cutting planar surfaces with a planar stencil surface in VTK

The Visualization Toolkit (VTK) is an open source, freely available software system for 3D computer graphics, image processing and visualization. VTK consists of a wide variety of visualization algorithms including advanced modeling techniques such as implicit modeling, polygon reduction, mesh smoothing, cutting, contouring and Delaunay triangulation. Through collaboration with various government and industry partners, Kitware continues to maintain and enhance VTK’s capabilities. This report details a useful addition to the Visualization Toolkit brought about by a unique requirement of climate data visualization.

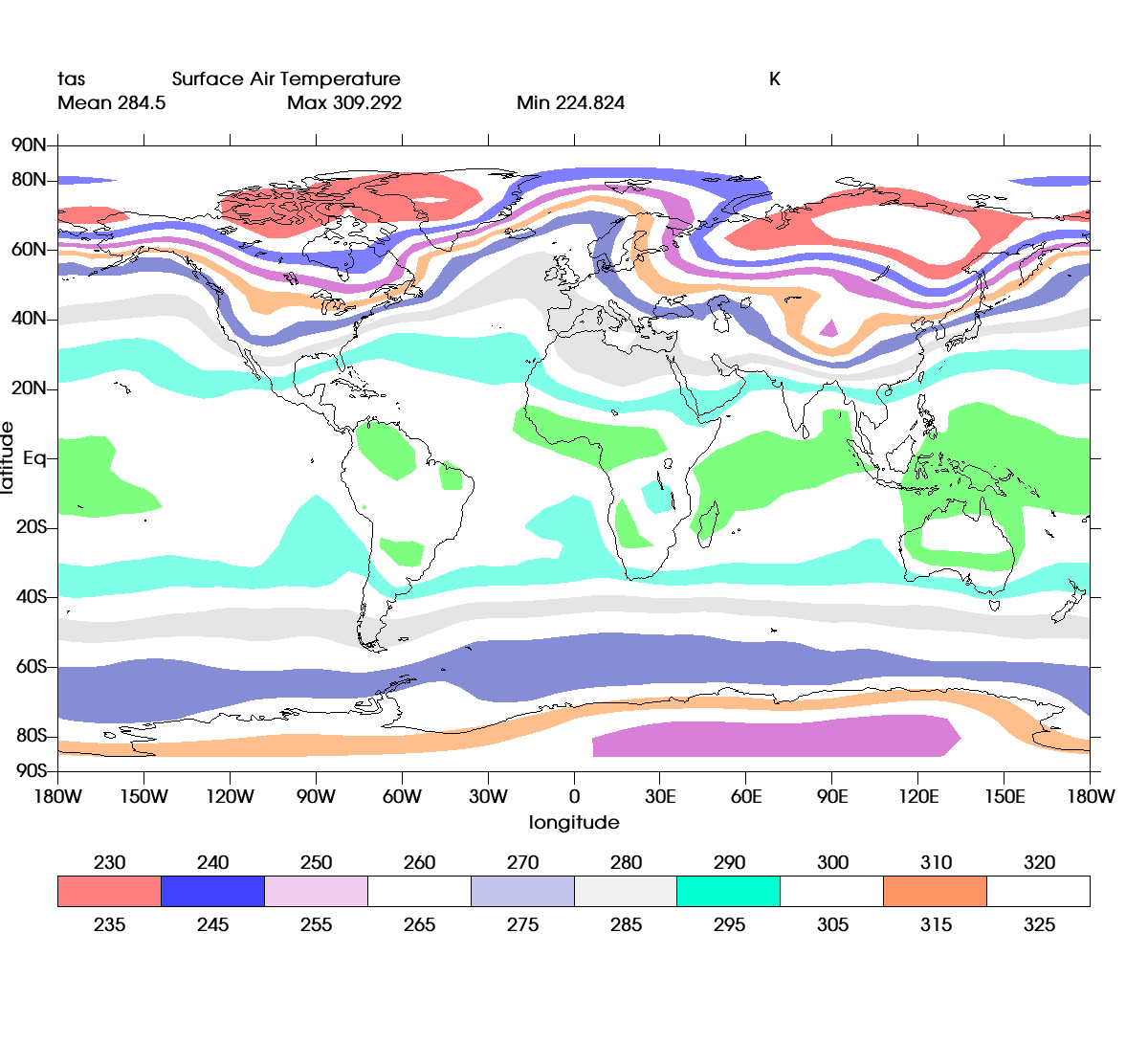
UV-CDAT (Ultrascale Climate Data Analysis and Visualization) is a framework developed at the Lawrence Livermore National Laboratory (LLNL) for analysis, visualization and management of large scale distributed climate data. The visualization component system (VCS) of UV-CDAT uses VTK as the data processing and visualization backend. UV-CDAT is used by climate scientists to visualize different parameters of massive climate datasets using different techniques like contour, heatmap, vector, and streamline plots along with volumetric display.

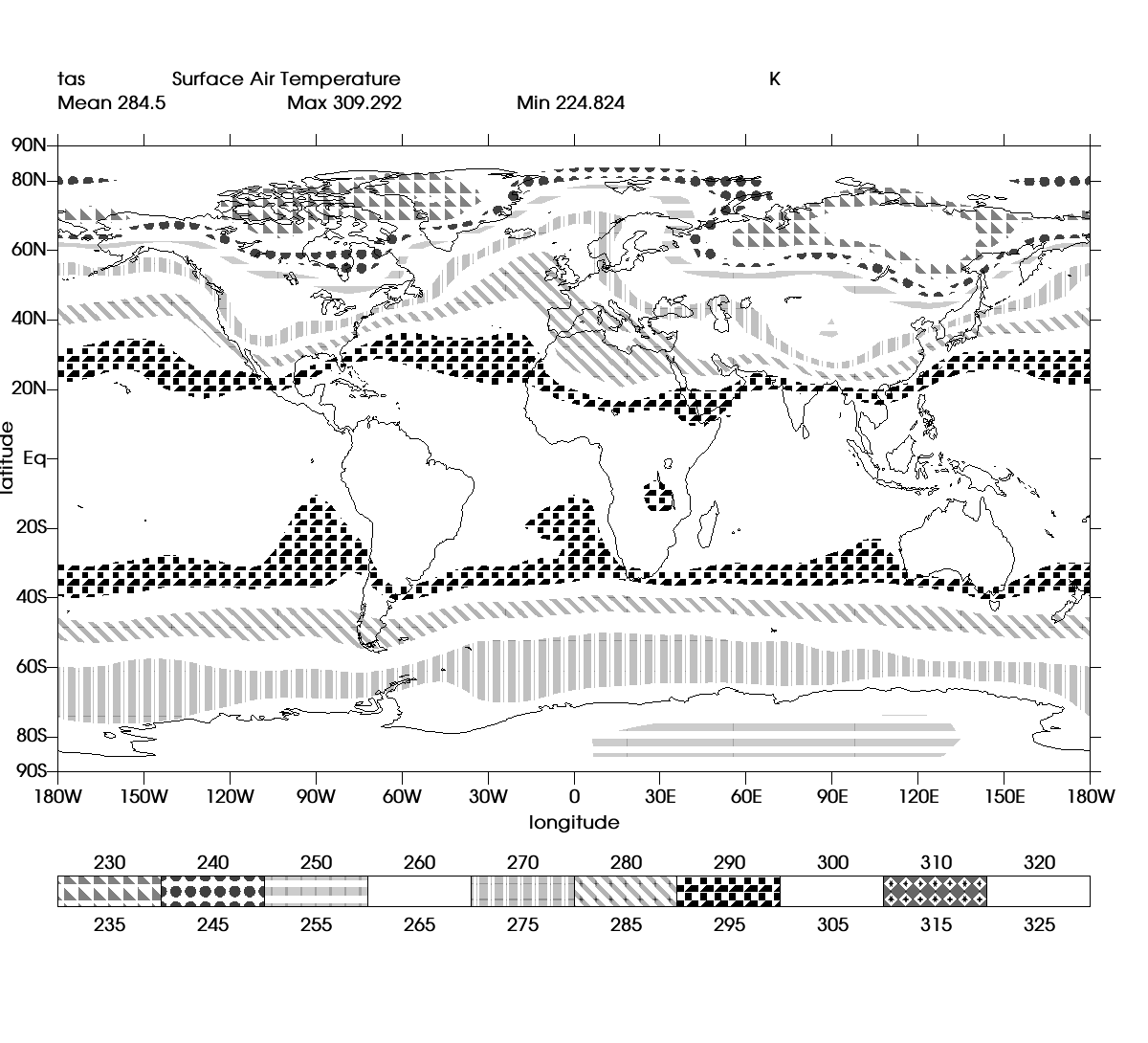
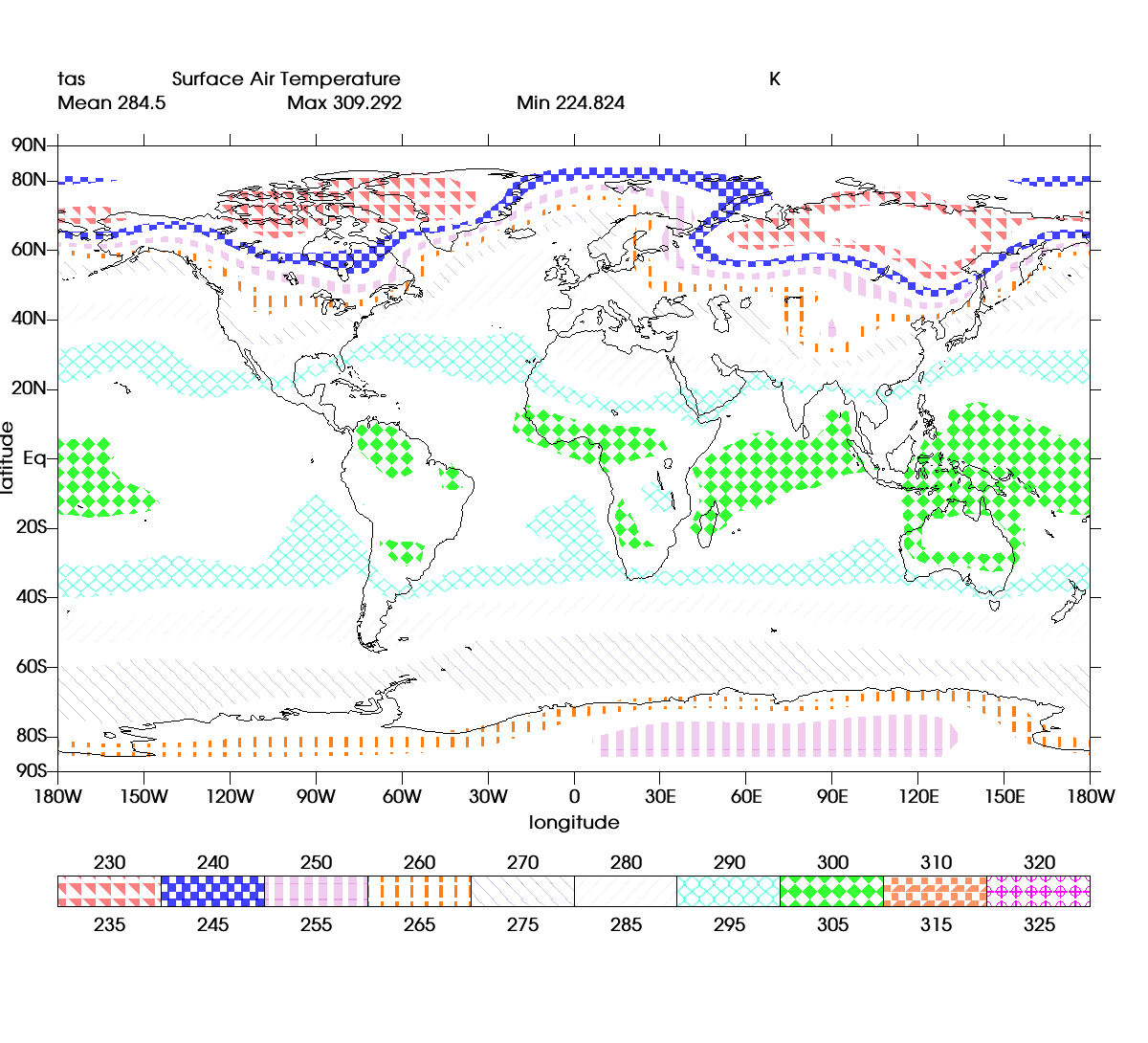
An important element of climate data plots involves delineating different regions of the dataset using colors, patterns and hatches. A pattern in UV-CDAT is a regular black shape repeated over the expanse of the surface, while a hatch is colored pattern. VTK supports mapping point and cell scalar values to colors using lookup tables. However, filling regions with patterns / hatches required an additional data processing pipeline:

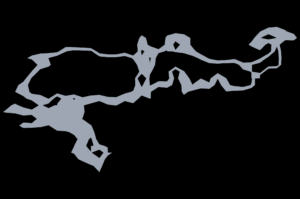
1. A plane surface with glyphs matching the expected pattern is created.

2. The plane is then cut to shape using the data region as a stencil.

3. The cut plane is then rendered as an overlay over the dataset

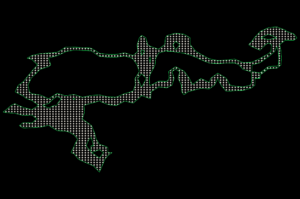
The second step in the above pipeline turned out to be a difficult step where in accurate cutting of lines, triangles and polygons is required to ensure the patterned surface fits within the data region. While VTK consists of many different ways of clipping vtkPolyData, including

1. 1. • vtkBooleanOperationPolyDataFilter extracts intersection of two different surfaces but requires the surfaces to be distinct in bounds. Stenciling out triangulated geometry is not supported.
      • vtkClipDataSet in combination with vtkImplicitDataSet could be used to clip the patterned surface with an implicit function derived from the region surface. However, this is an approximation technique and the result is not ensured to accurately fit within the boundaries of the region dataset.

vtkCookieCutter

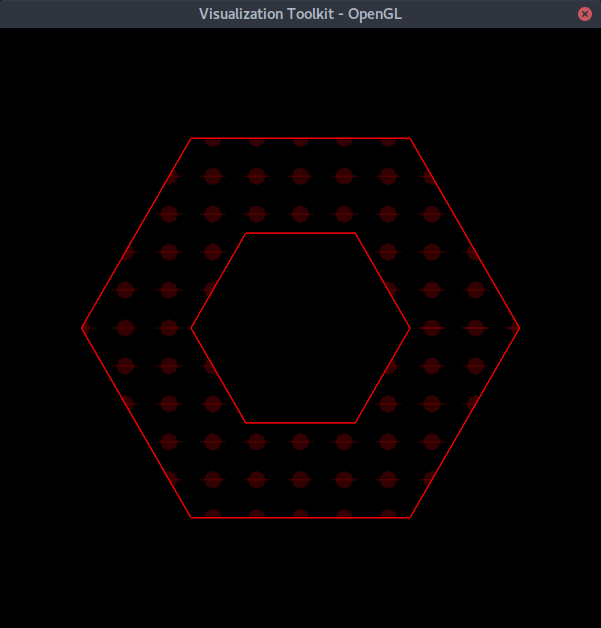
To provide satisfactory results, we decided to implement a specialized class to perform the  cutting operation described previously. The filter crops polygonal data (vertices, lines and polylines, polygons, and triangle strips) positioned in a 2D plane with one or more loops. Both the loop and polygonal data can be non-convex. Note however that the loops are presumed not to contain internal holes.

Like many geometric processing algorithms, often the basic concepts are simple while the implementation requires significant head scratching to get right. For example, numerical situations such as degeneracies can confuse a naive algorithm, and it’s also important to note the that the intersection between two concave polygons may produce multiple polygons on output. In the algorithm we implemented, we found that operations performed in the parametric space were much more reliable, as processes involving sorting, merging, and traversing output loops (i.e. polygons) are greatly simplified by sorting intersection points around the perimeter of the cutting loop (and polygonal primitives). Also in/out tests are critical to the final result, fortunately VTK already had a decent implementation and we were able to leverage that capability.

A significant challenge to the algorithm is obvious from the earlier image showing the complex surface to be patterned. Note that the surface contains several interior holes, something which our algorithm does not support. However, the patterned surfaces are actually made up of simpler primitives such as triangles. Thus our solution was to treat each primitive making up the patterned surface as a separate loop which in turn was used to process the entire glyph field. At the conclusion of processing the result was that the glyphs were often cut into many pieces, but when assembled (i.e., rendered together) appeared to be whole.

Performance on our data was acceptable using some geometric shortcuts like bounding box tests to accelerate computation. Note however that the algorithm could be easily sped up/threaded, including accelerating in/out tests and employing parallel glyph processing. We are hoping that the right customer or open source contributor will take this on.

We would like thank the Lawrence Livermore National Laboratory and the UV-CDAT lead Dean Williams and Charles Doutriaux for sponsoring this work.