Fluid Simulation in iMSTK using Smoothed-Particle Hydrodynamics (SPH)

Introduction

Smoothed Particle Hydrodynamics (SPH) is one of the widely used methods for simulating fluid flow (and solid mechanics) in distinct areas such as computer graphics, astrophysics, and oceanography among others. SPH is a mesh-free Lagrangian method that employs a kernel function to interpolate fluid properties and spatial derivatives at discrete particle positions (Figure 1).

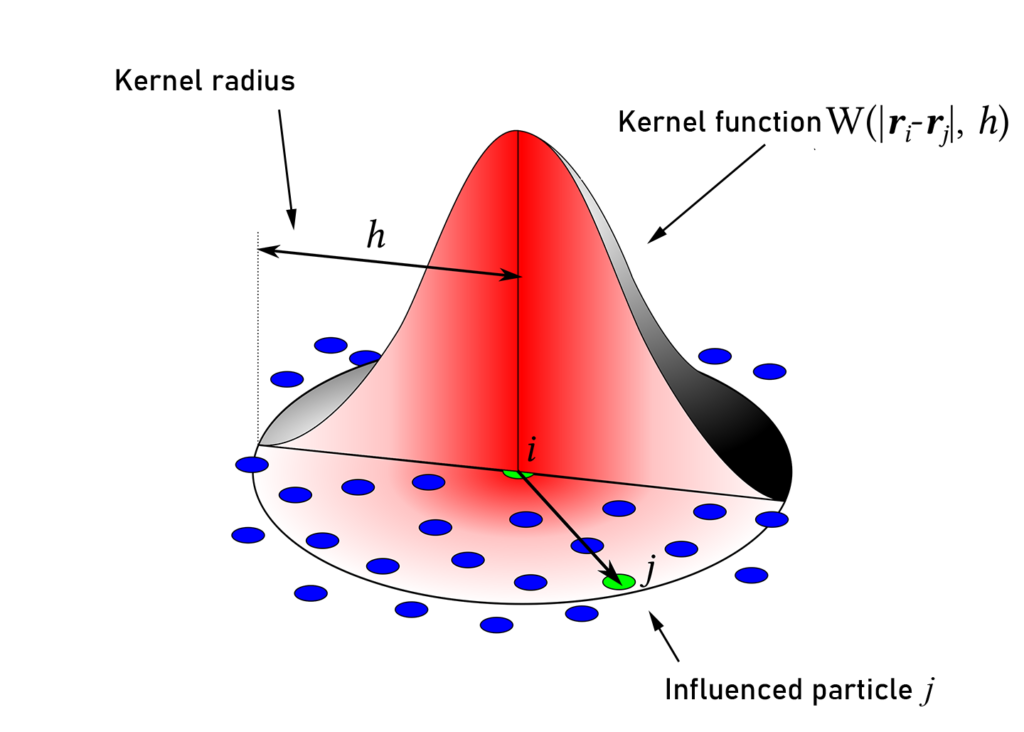
Owing to its simplicity and versatility, SPH has been studied and improved extensively, making it a reliable technique for physically-based simulations with a wide range of capabilities. Besides fluids, the state-of-the-art SPH formulations can model solids, fluid-solid interactions, as well as materials with phase transitions [1]. For more background on SPH and its applications in simulation, readers may refer to the review paper by Ihmsen et al. [2].

In this blog, we report the addition of SPH simulation capabilities into our Interactive Medical Simulation Toolkit (iMSTK). iMSTK is a C++ based free and open source toolkit that aids rapid prototyping of real-time multi-modal surgical simulation scenarios. Since the first release in December 2018 ([3], [4]), iMSTK has seen many improvements and feature additions. The addition of SPH will allow for more accurate fluid simulation often required in surgical simulation applications. The current formulation can model fluid with varying viscosity and surface tension and one-way solid-fluid interactions.

Implementation details

Real-time surgical simulation applications using iMSTK favor speed and robustness while accepting liberal tolerances on accuracy. Besides these prime objectives, our goal of a simplistic API has informed us in the design choices for the current implementation. The SPH model in iMSTK is a form of Weakly Compressible SPH (WSPH) introduced by Becker and Teschner [5], but with a number of modifications. In particular, we employ their proposed momentum equation for acceleration update and Tait’s equation for pressure computation. However, we utilize two different functions for kernel evaluation and evaluation of kernel derivatives, similar to Muller et al. [6]. In addition, we use a variant of XSPH [7] for modeling viscosity that is computationally cheaper than the traditional formulation. The forces of surface tension are modeled using a robust formulation proposed by Akinci et al. [8] allowing simulation of large surface tension forces in a realistic manner.

During the simulation, each of the SPH particles needs to search for its neighbors within a preset radius of influence of the kernel function (see figure 1). In iMSTK, the nearest neighbor search is achieved using a uniform spatial grid data structure or using spatial hashing based lookup [9]. For fluid-solid interaction, the current implementation only supports one-way coupling in which fluid particles are repelled from solids upon collision by penalty force generation.

Example

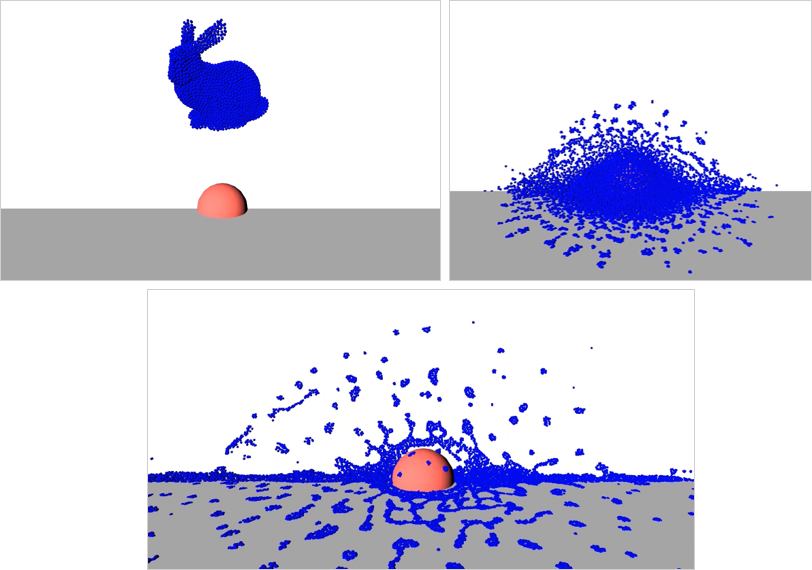
We provide several SPH fluid examples in the iMSTK repository source code. Below is a code snippet to demonstrate how to create and configure an SPH simulation:

Some simulation examples using SPH are showed in the video below. Note that the video was not recorded directly from the simulations at the actual speed.

Future work

Serial implementation of SPH can achieve interactive frame rates with up to a few thousand particles. We are currently adding a parallel execution model in iMSTK, which can significantly accelerate the computation in the modern multi-core computer systems. Performance of our parallel SPH solver will be reported in a follow-up blog. We are also working on adding screen-space fluid rendering [10] to VTK for use in iMSTK via VTK rendering back-end. For the next iMSTK release, we will explore potential improvements to SPH such as adaptive penalty forces for more stable fluid-solid interaction, two-way fluid-solid coupling, and dynamic particle addition and deletion.

References

[1] Barbara Solenthaler, Jürg Schläfli, and Renato Pajarola. “A unified particle model for fluid–solid interactions”. Comput. Animat. Virtual Worlds, 18, 1 (February 2007).

[2] M. Ihmsen, J. Orthmann, B. Solenthaler, A. Kolb, M. Teschner, “SPH Fluids in Computer Graphics”. In Proceedings of Eurographics 2014.

[3] https://blog.kitware.com/new-software-from-kitware-virtualizes-medical-education-and-training

[4] https://blog.kitware.com/introducing-imstk-part2

[5] Markus Becker and Matthias Teschner, “Weakly compressible SPH for free surface flows”. In Proceedings of the ACM SIGGRAPH/Eurographics symposium on Computer Animation, 209-217 (2007).

[6] Matthias Müller, David Charypar, and Markus Gross, “Particle-based fluid simulation for interactive applications”. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer Animation, 154-159 (2003).

[7] Hagit Schechter and Robert Bridson, “Ghost SPH for animating water”. ACM Transaction on Graphics, 31, 4, Article 61 (July 2012).

[8] Nadir Akinci, Gizem Akinci, and Matthias Teschner, “Versatile surface tension and adhesion for SPH fluids”. ACM Transaction on Graphics, 32, 6, Article 182 (November 2013).

[9] Teschner, M., Heidelberger, B., Müller, M., Pomeranets, D., and Gross, M, “Optimized spatial hashing for collision detection of deformable objects”. Proc. VMV, 47–54.