Novel Discretization and Formulation Support in VTK and ParaView
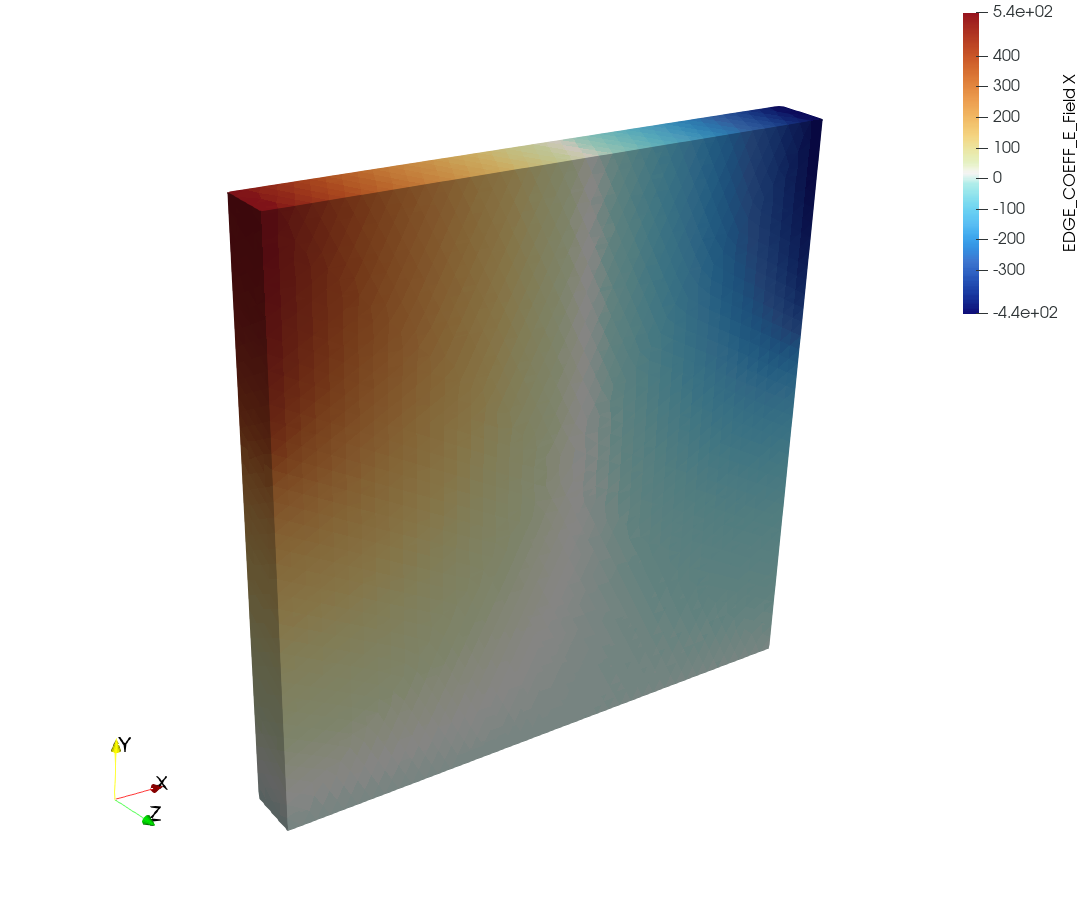
VTK and ParaView have a huge library of visualization tools built on a data model that progressively adds conceptual assumptions based on how the data can be represented; the more information you can provide about your data, the more efficient the tools can be. For example, vtkDataObject assumes only that data can be represented by a collection of arrays; vtkDataSet adds the assumption that data has geometric points which are connected by cells while vtkTable instead assumes data is in columns of data that all have the same number of rows. We are adding a new class, vtkCellGrid, to address a large range of novel discretizations.
The figure to the left shows concrete examples of what is supported by VTK’s traditional data model: the leftmost quadrilateral cells show a value at each point (p₀, p₁, p₂, p₃) while the rightmost shows one value per cell (c₀), which assumes the single value is constant over the cell.
The right two cells below show newer models: a single value per edge (ei, immediately to the right) or some number of quadrature-point values (qi) per cell, which may not match the shape function’s polynomial order (far right).
As applications that produce science and engineering data – such as simulations and experimental apparatus – have evolved, the conceptual models of the data they provide have changed. Many of the assumptions VTK and ParaView were engineered to take advantage of – such as equivalence between a point- or cell-centered array and the function over space the array values specify – are not relevant to these new forms of data. The problem is that there has been an explosion of simulation solvers, functional approximations, data fitting techniques, experimental techniques and more. The word cloud below summarizes just some of the novel approaches we have been asked to support.

If there were just a few new techniques, the community around VTK and ParaView would simply have added them to the existing repertoire of file types and algorithms they support.
Instead of attempting to support all of these disparate approaches as patchwork additions in VTK’s existing inventory of data representations or unify them into a new hierarchy of conceptual assumptions, we have developed vtkCellGrid, which we’ll refer to as a “cell grid.” It does not encode assumptions via class inheritance.
A key feature of cell grids is that conceptual assumptions about data no longer use C++ inheritance to refine the data model.
Eliminating inheritance as a means of modeling conceptual assumptions simplifies representing data that was difficult to work with before cell grids were introduced. We’ll discuss how we accomplish this in the text below. But first, let’s look at an example of the type of problems novel discretizations present.
Above is the output of EMPIRE, a discontinuous Galerkin solver written by Sandia National Laboratories, simulating an electron beam traveling in a vacuum from left to right across the domain with about 60,000 tetrahedra. There are discontinuities at finite element boundaries which were not easy to model in VTK before the introduction of cell grids. The electric and magnetic fields are represented with Nédélec (and Thomas-Raviart) elements that store coefficients on edges (and faces) rather than at element corners, which were also not able to be precisely represented in VTK before the introduction of cell grids. But cell grids solve far more problems than this.
One issue the example above presents is how continuity between finite elements is modeled. Previously, discontinuities between elements implied that the discontinuous function was constant over each element or the elements did not share any connection to neighbors. New formulations recognize that many physical systems need continuity of a function along a path or normal to a surface; they admit varying values over neighboring finite elements and allow discontinuities normal to edges or tangent to surfaces. Math models that use Gauss’s Theorem or Green’s Theorem to compute flux through a surface or closed loop can be discretized with elements that force continuity in certain directions and allow discontinuity in others that make these easy to compute. Besides continuity, integration via quadrature/cubature in the Nédélec and Thomas-Raviart formulations Sandia uses has been reduced to simple addition – making conservation of energy, charge, or other important quantities immune to integration error.
But there are many other formulations. Some formulations use bounded derivatives that provide a convex-hull property so it becomes easier to robustly find zeros of fields. Some formulations ensure vector fields can be separated into portions with and without vorticity. Some provide solution fields that can model singularities while remaining numerically stable. Some have been created to exactly match CAD models’ complex shapes so that solution fields are faithful to the domain shape (eliminating discretization error). Some formulations, instead of representing a field at fixed points in time, can model a field’s behavior over an interval of time. Many application areas drive the development of these formulations; particle swarms admit simulations where materials change phase or composition without explicitly modeling the interfaces of these changes. Modeling cracks in solid materials have driven boundary matching, XFEM, and bulk quantity approximation/multiscale modeling. All of these advances introduce complexity in visualization and analysis tools like VTK.
Supporting all of the different modeling techniques being developed is a software engineering challenge, not just a numerical methods challenge.
One of the existing ways VTK has dealt with complexity is to separate itself into modules that can be eliminated from builds when functionality is unneeded. For example, if your application doesn’t need to read and write Exodus-formatted data (or GDAL data, or PLY data, etc.) you can simply disable the modules that support these formats.
VTK – through the new vtkCellGrid class – now uses this same pattern for cells so you can implement your own cell types in a separate (and even external) VTK module and make existing vtkCellGrid algorithms work with them. Previously, every new data model had to exist inside the CommonDataModel module.
Cell types don’t make many assumptions about how your data is represented – a cell is just some object that has a shape attribute (i.e., it covers some region of space described by a function) and any number of other attributes (functions that return 1 or more values at each point in space). Cell grids are just containers of three types of data: array groups (named Attributes to match terminology from vtkDataObject), Cells (a metadata entry per type of cell), and CellAttributes (that model functions defined over the underlying space of the cells):
How does this allow your cell types to work with existing vtkCellGrid algorithms? The “secret sauce” (not so secret since VTK and ParaView are open source) is the query+responder pattern that cell grids use; a query class is created that is relevant to some visualization task such as rendering, picking, transforming, or isocontouring. Then, a responder class is registered to the query which indicates it can perform the query given a particular type of input data. When you ask ParaView to perform a visualization operation, ParaView asks VTK what responders are available for the user’s query. An example of how an algorithm might work for a cell grid containing both DGHex and DGQuad cells is shown below:
The VTK algorithm’s RequestData() method prepares a query (say to deform the shape of the input cells), then asks the cell grid to process the query. For each type of cell in the cell grid, it locates and invokes a responder registered for the query+cell-type combination. Finally, the query is given an opportunity to finalize the resulting cell grid. The developer of the algorithm doesn’t need to know how each cell type will respond to the query. The responders only need to know how to process one type of cell. The registration system allows external modules to add new cell types, new query types, and new responders for existing and/or new queries.
This means every science and engineering application can provide its own data formats (cell types), analyses (responders), and algorithms via additional VTK modules. You can implement responders to the queries your audience needs and add to it over time. ParaView and VTK make it easy to expose and explore your data in world-class applications.
Beyond a container for arbitrary data models, support for fixed-shape, non-isoparametric cells with discontinuities is provided.
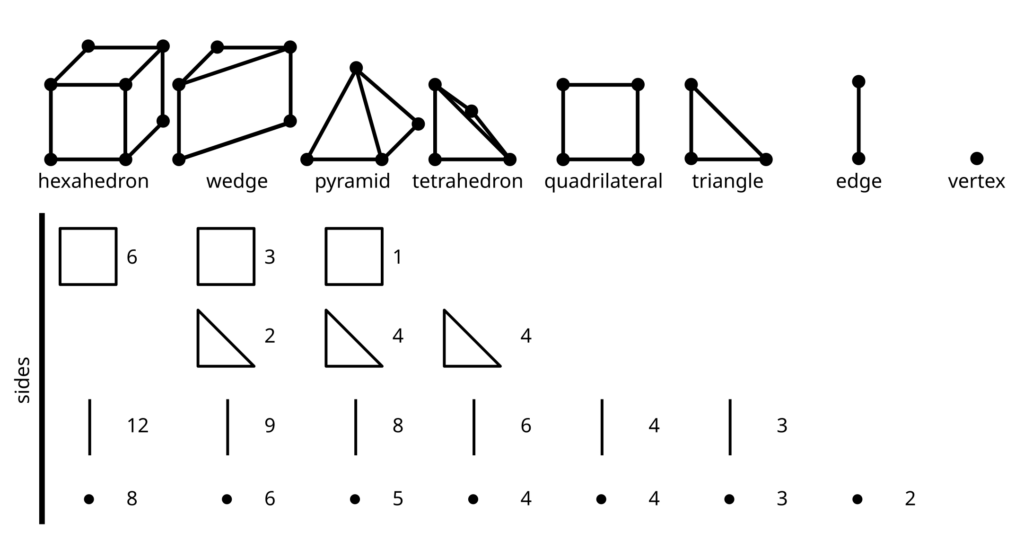
Besides providing an improved framework for representing arbitrary discretizations and function spaces, Kitware has implemented new cell types with a fixed set of shapes (hexahedra, tetrahedra, wedges, pyramids, quadrilaterals, triangles, edges, and vertices) that provide interpolants in H-grad (a.k.a. Lagrange), H-div, H-curl, and constant function spaces.
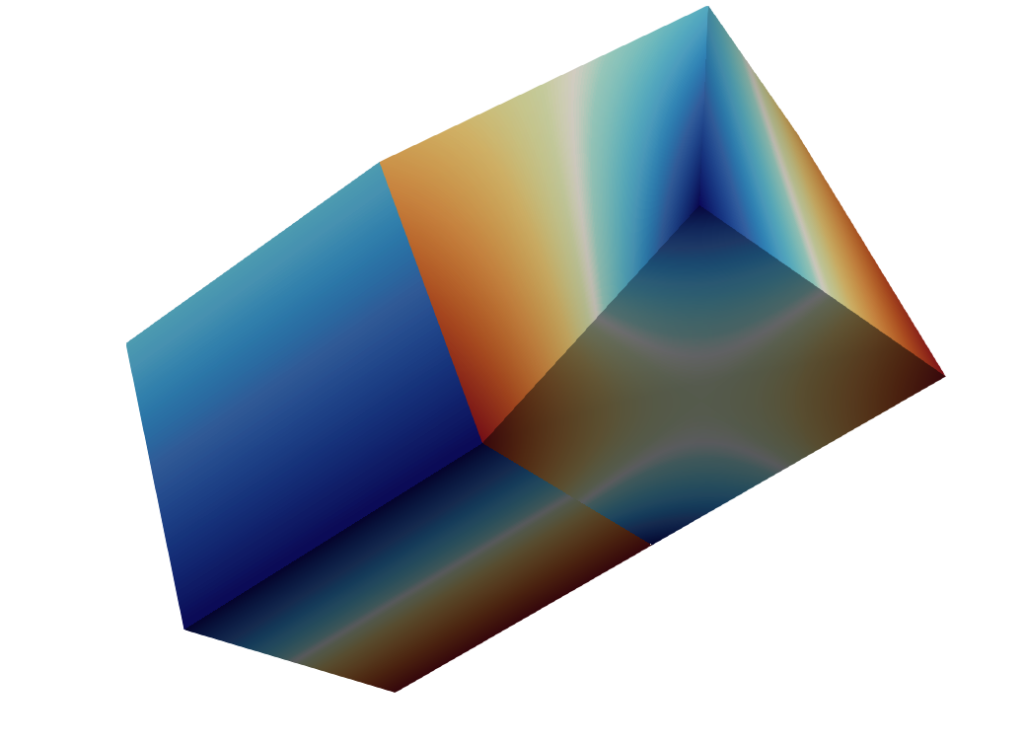
These cells are non-isoparametric (the attributes defined on each cell may have different interpolants and polynomial orders). For example, below are a pair of linear-shape hexahedra with discontinuous function values; and a single wedge with a quadratic shape polynomial and an order-1 H-curl field (shown with both arrow glyphs and color (vector magnitude).

More Information
VTK’s documentation discusses cell grids in some detail; we also have a discourse topic documenting the progress of our design rationale in more detail. If you have technical questions, please post them on the discourse site. If you are interested in having Kitware advise, collaborate, or develop visualization and analysis software using cell grids, please start a conversation with us!
Acknowledgements
This work was funded in part by Sandia National Laboratories.
Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525.
This work was also funded in part by the Data Analysis and Assessment Center of the United States Department of Defense High Performance Computing Modernization Program.
This post has been reviewed and approved as SAND2024-14524O.