New VTK Source for Generating Different Cell Types
The linear-edge cell types supported in VTK and ParaView are used all the time and have seen extensive use. While many people are aware of the higher-order cell types available in VTK, they certainly see much less use and testing. The newly added vtkCellTypeSource aims to improve on this by providing a simple mechanism to generate a wide variety of unstructured grid cells. Currently, it can generate linear and quadratic versions of lines, triangles, quadrilaterals, tetrahedra, hexahedra, wedges or pyramids as well as a cubic line. The design of the source is meant to encourage other unstructured grid cell types to be supported in the near future as well. The source can produce pieces of data (i.e. partitions appropriate for parallel processing pipelines) and has proper connectivity (i.e. water-tight). To ensure that the source works properly, a test (vtkFiltersSourcesCxx-TestCellTypeSource) was added to VTK that verifies that the proper number of points and cells are generated for each available cell type and that the sizes of the generated cells are correct. The test already showed incorrect functionality in the Triangulate() method for the quadratic hexahedra, quadratic pyramid and quadratic wedge.
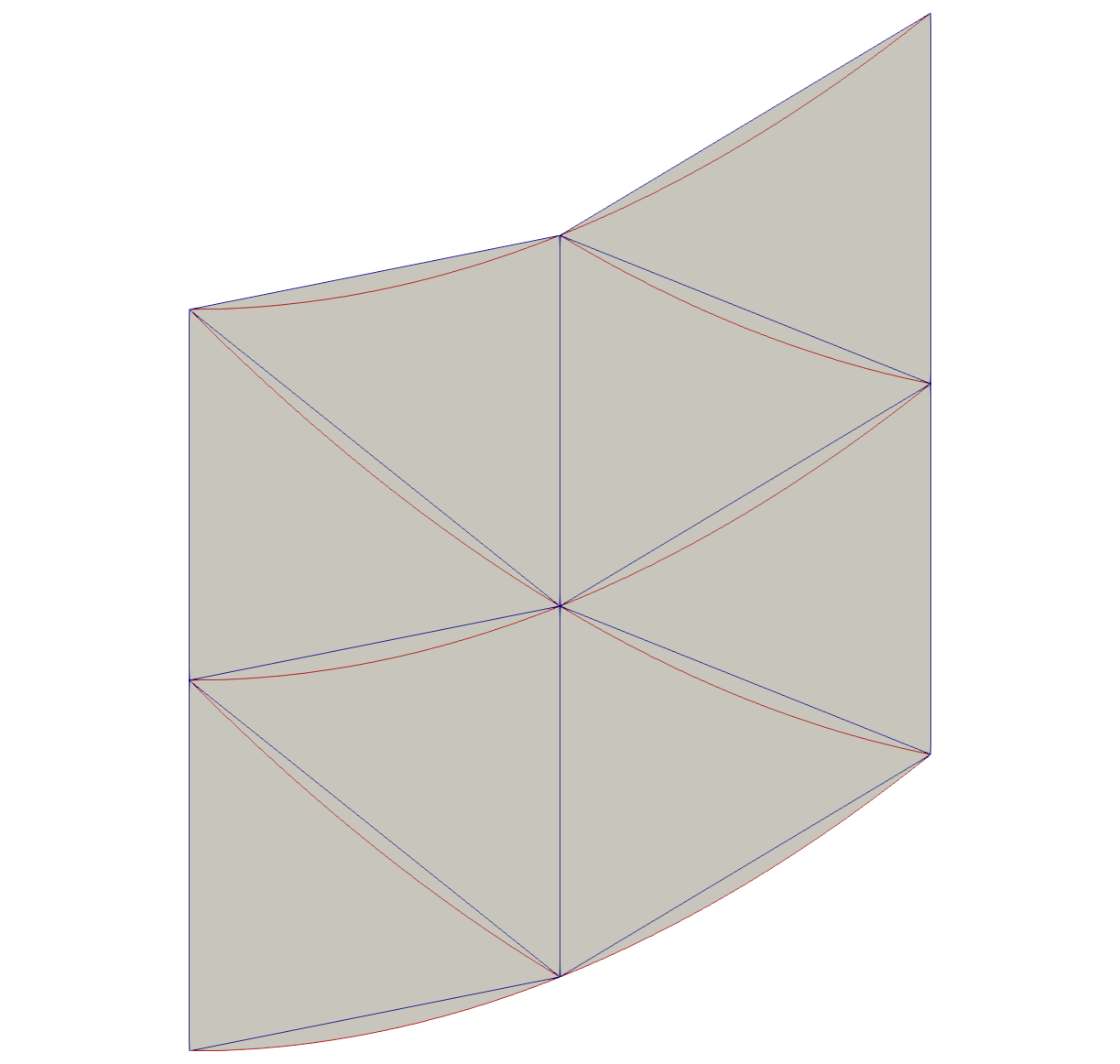
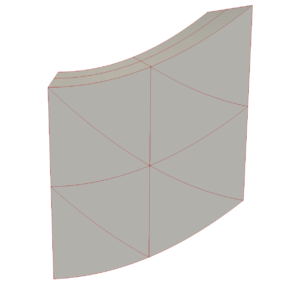
In ParaView, this source is called the Unstructured Cell Types source and will be in the upcoming ParaView 5.4 release. While the generated data set will still have straight-edged cells even for the non-linear cells, the Calculator filter can be used to modify the data set’s geometry. In the image below I generate 16 quadratic wedges with the Unstructured Cell Types source and then use the Calculator filter with “coordsX*iHat+(coordsY+coordsX*coordsX*.2)*jHat+coordsZ*kHat” as the expression and check the Coordinate Results option. To better show the curvature of the quadratic wedges, I also set the Nonlinear Subdivision Level to 4.
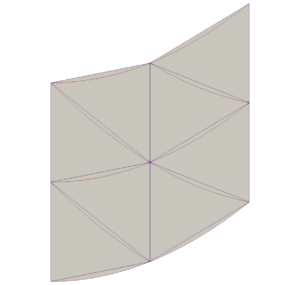
Comparing this data set to what I would get if I had the Unstructured Cell Type source generate linear wedges instead is shown in the next image. Here, the blue edges are the edges of the linear wedges and the maroon edges are the edges of the quadratic wedges.
This addition to VTK and ParaView was funded by Sandia National Laboratories.
Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525.
Thank you for writing this up, it prompted me to revisit viewing an older unstructured mesh that gave me problems in the past. This time, I was able to load my model with second-order hexahedra (type 25) and everything looks good. When I set the nonlinear subdivision level to 4, as you did, I see reasonably smooth behavior. However, two questions:
(1) Setting subdivision to 0 makes the model appear linear (more coarse than reality); is this expected?
(2) Is there a way to avoid manipulating the subdivision level and instead having ParaView display curved edges according to the order of the element (0, linear, straight and 1, quadratic, smooth)? It seems like this would give the most faithful visualization of the mesh.
Thanks,
Joel
Oops, that should have been: 1, linear, straight and 2, quadratic, smooth…
Hi Joel,
The way that ParaView (and VTK underneath the covers) works for visualizing higher order cells is by subdividing them. Thus, the closer you want these curved cells to represent the true geometry the more you will have to refine them. This is the intent of the subdivision level option. The reason we have this option is that the subdivision can be an expensive compute operation as well as using more memory. For example, for your second order hexahedra using a subdivision level of 2 would increase the amount of cells by a factor of 8 (though this would just be done for the cells on the surface of your filter output). Automating the selection of an appropriate subdivision level in an efficient manner is certainly doable but not quite trivial.