iMSTK Integrates Pulse Physiology Engine

Motivation

Simulation-based training has become an essential part of medical education. Modern-day virtual trainers go beyond knowledge delivery or skill and procedural training in the clinical sense. They are being used for improving team communication and coordination skills in crisis management scenarios. iMSTK provides the essential building blocks needed to prototype physics-based virtual reality (VR) multimodal (visual, haptic, aural) trainers of all stripes. Pulse physiology engine, also led by Kitware, simulates human physiology using a low-cost, 0-D modeling approach. With the integration of Pulse, iMSTK’s users can couple human physiology into surgical scenarios.

Traditionally, VR procedural trainers focus on delivering high-fidelity simulation of a critical phase of the surgery. Procedural trainers model the environment and interactions in the surgical corridor with high precision while ignoring the rest. Event-driven, scenario-based trainers on the other hand focus on interpersonal communication in the OR, imparting didactic knowledge, team coordination, and crisis management (e.g. iMSTK-based OR fire simulator). While the use of physiological sign monitors is common in the latter, this integration provides the ability to couple the events from the high-fidelity simulation of the former with human physiology. The use case detailed later in the blog demonstrates precisely this. First, we describe the details of integration and specific improvements to the fluid models in iMSTK below.

Pulse physiology in iMSTK

A new dynamical model-PhysiologyModel, has been added in imstk to simulate human physiology. The following code snippet shows how to create and configure this physiology model.

// configure the Physiology model    
// Set the base physiologic state to available preset
imstkNew<PhysiologyModelConfig> physiologyParams;
physiologyParams->m_basePatient = PatientPhysiology::StandardMale;

// Create a Physiology model
imstkNew<PhysiologyModel> physiologyModel;
physiologyModel->configure(physiologyParams);

// Crete a physiology scene object
imstkNew<PhysiologyObject> physiologyObj("Human physiology");
physiologyObj->setDynamicalModel(physiologyModel);

Actions in the Pulse engine allow users to specify external insults or interventions such as hemorrhage, airway blockage, or cardiac arrest. PhysiologyModel can accept ‘actions’ that can be added (or removed) at runtime.

// Create an external hemorrhage on the right leg
imstkNew<HemorrhageAction> hemorrhageAction(HemorrhageAction::Type::External,
  "VascularCompartment::RightLeg");

// Add a hemorrhage action to the model
physiologyModel->addAction("Hemorrhage", hemorrhageAction);

Data from the current physiologic state can be retrieved via Pulse compartments which can be obtained in imstk from the physiology model. For example, to obtain the blood inflow rate in the right femoral artery one may call

physiologyModel->getCompartment(PhysiologyCompartmentType::Liquid, "VascularCompartment::RightLeg")->GetInFlow(VolumePerTimeUnit::mL_Per_s)

Showcase: Arterial bleeding induced hemorrhage

We demonstrate a use case where arterial bleeding, simulated using iMSTK, is coupled to the hemorrhage model of the whole body physiology delivered by Pulse.  The high-definition bleeding simulation model informs the low-definition physiology model and vice versa. Opportunities for such coupling are plenty. It allows the procedural simulators the ability to present patient-specific, real-time valid physiological responses to events induced by user actions (e.g. damaging the femoral artery) on the high-fidelity models. This expands the purview of the simulators with regards to training and renders them holistic.

Before we attempted this use case, we had to improve numerous aspects of the fluid model in iMSTK to accommodate the arterial blood flow (pipe flow) simulation. Below we provide details of the improved fluid model and its validation before proceeding to demonstrate the use case.

Improved SPH model to simulate pipe flow

iMSTK offers Smoothed Particle Hydrodynamics (SPH) for fluid simulation (see previous SPH blog). SPH is a mesh-free Lagrangian method that employs a kernel function to interpolate fluid properties and spatial derivatives at discrete particle positions. SPH is a widely used method to simulate fluid flow in a wide range of applications including computer graphics, astrophysics, and more recently, arterial blood flow. The lack of a fixed computational grid makes SPH an ideal candidate to simulate free-surface flows where the computational domain may not be fully occupied with the fluid. SPH is also widely used to produce high-quality visualizations (Monaghan, 2012). iMSTK’s current SPH model required the following key improvements to simulate pipe flow:

• Improved stability: To maintain ordered movement of particles and keep particles from forming high-density clusters, we implemented the XSPH method (Monaghan, 1992; Ozbulut, Yildiz and Goren, 2014) that averages a particle’s velocity based on the velocity of its neighbors. By preventing high-density clusters, this method improves stability and allows for simulations with higher velocities and larger time steps.
• Better time-stepping: The governing equations modeled by SPH are now stepped in time using a second-order leap-frog scheme for improved stability (Ozbulut, Yildiz and Goren, 2014).
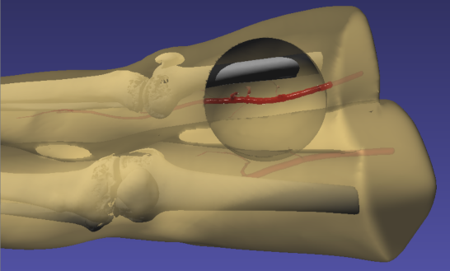
• No-slip boundary conditions: In blood flow simulations, a no-slip boundary condition (i.e., no relative motion between the fluid and the wall at the fluid-wall interface) at the wall is critical for accurate pressure and flow rate calculations. To implement no-slip boundary conditions, vessel geometries are hollowed and filled with fluid particles. The walls are padded and filled with layers of stationary SPH particles (see Figure 1). The wall particles are regular SPH particles except that their movement is restricted. This method allows for a continuous density gradient and does not require significant special treatment of wall particles. The minimum thickness of the padded region is the kernel radius in order to avoid truncated kernel integrations (Al-Saad, Kulasegaram and Bordas, 2016).
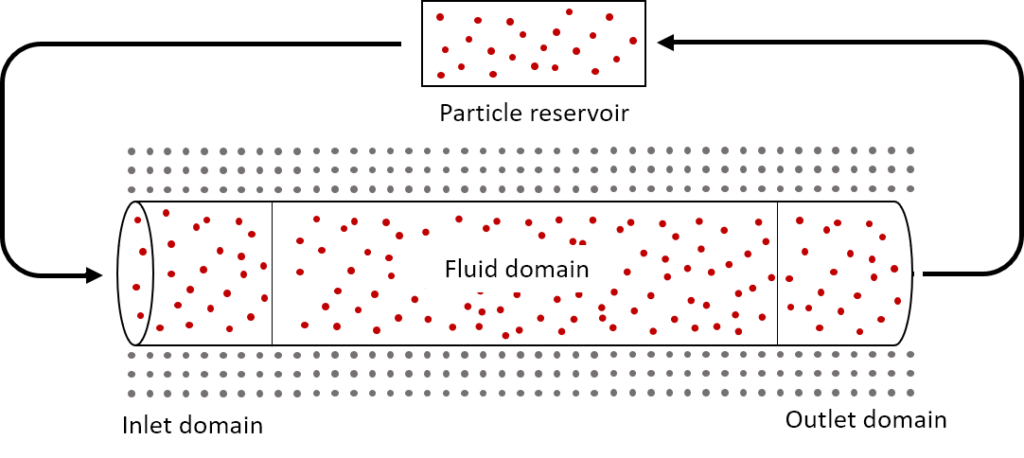
• Inlet and outlet boundary conditions: Accurate treatment of inlet and outlet boundary conditions is an active area of research today. We implemented the boundary conditions based on a recent method developed by Alvarado-Rodríguez et al.  (2017) that uses an inlet domain, outlet domain, and particle reservoir (Figure 1). Particles in the inlet domain are subject to the flow rate at the inlet, and particles in the outlet region are subject to either pressure or flow rate at the outlet. If a particle moves from the inlet into the fluid domain, that particle is replaced by a particle from the reservoir. If a particle leaves the outlet domain, that particle is placed back into the reservoir, thus ensuring that the reservoir contains enough particles to replenish the inlet domain. Particles in the inlet and outlet domains are treated as regular SPH particles, but particles in the reservoir do not interact with the fluid and are implemented simply as a storage method to avoid the use of dynamic arrays as particles enter and leave the domain. In grid-based methods, the mesh and number of fluid points are static, but in SPH vessel flow, the number of particles within the geometry can change at any time step. Thus, mass is not always conserved within the fluid domain but is generally conserved when the particles in the reservoir are accounted for.

Validation

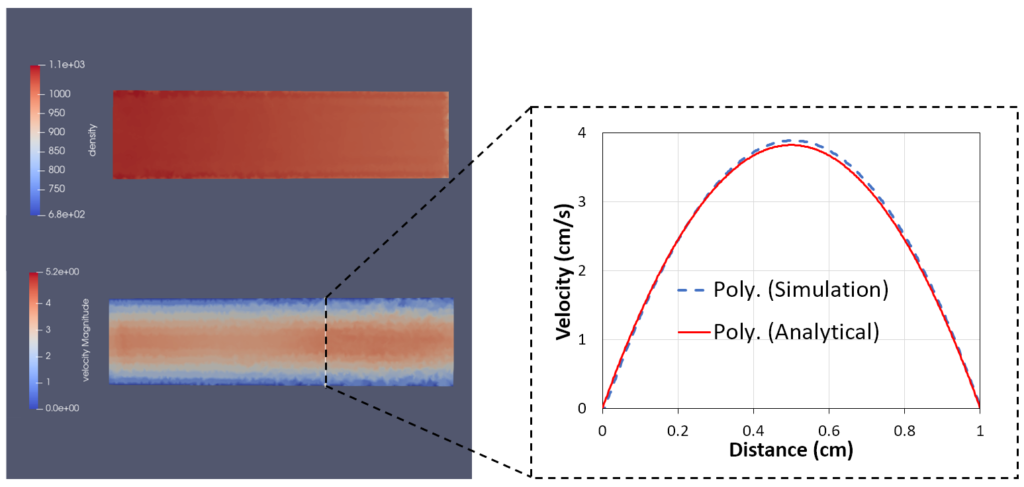
We validated the improved SPH model in iMSTK using several standard test cases whose solution can be expressed in closed-form (Figure 2). All test cases use the upgraded formulation for inlet and outlet boundary conditions and no-slip boundary conditions at the wall. Figure 2 shows the parabolic flow profile in a straight pipe in good agreement with the analytical solution.

Femoral artery injury-induced hemorrhage

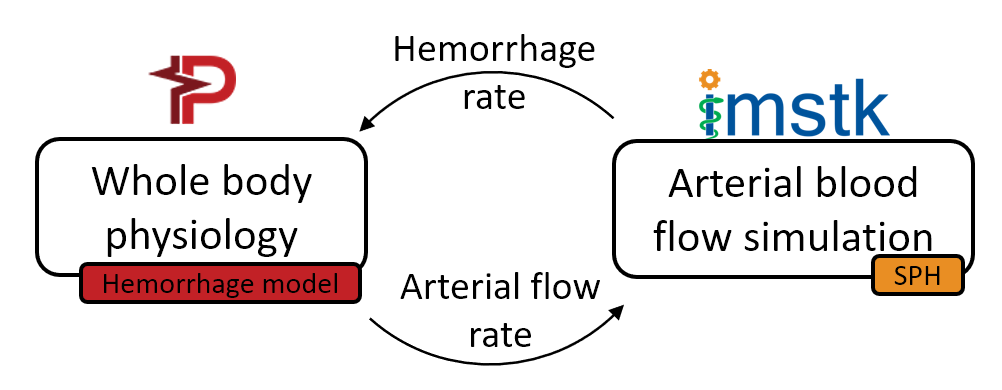
To simulate the effects of hemorrhage on patient vitals, we coupled the SPH model in iMSTK tasked to simulate the blood loss with the lumped parameter hemorrhage model of the Pulse engine. Pulse represents the entire cardiovascular system with electrical circuit analogs where resistors represent resistance to fluid flow and the capacitors represent compliance of blood vessels. We coupled the high-fidelity local SPH model to simulate blood flow and leakage from femoral arteries with a low-fidelity yet global (whole-body) cardiovascular model of Pulse. A section of the femoral artery whose geometry is derived from publicly available patient CT datasets is used to simulate arterial blood flow in iMSTK. Artificial damage is induced (see Figure 3) that leaks the blood, eventually leading to a hemorrhage.

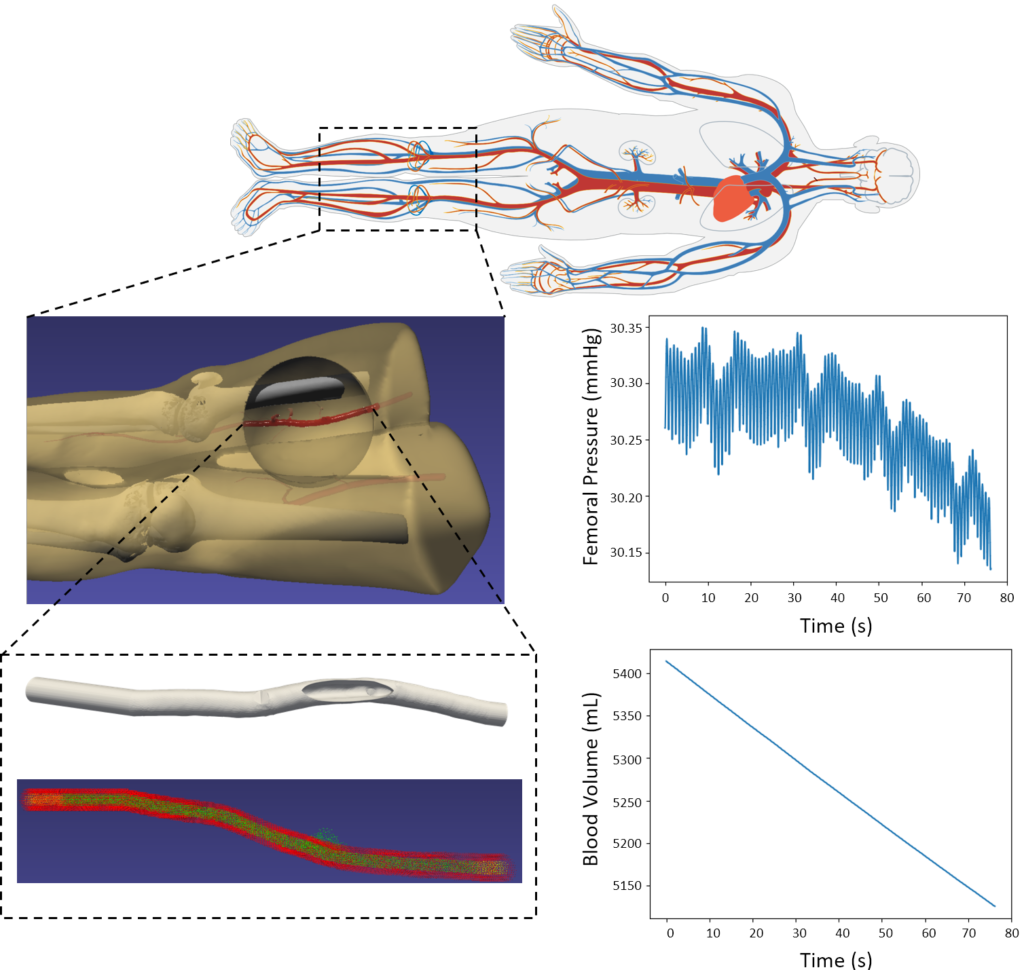
The two-way coupling between these models is achieved at each time step of the simulation by (a) computing the blood loss from the SPH model and passing it on to the Pulse’s hemorrhage model and (b) using the femoral artery flow rate in Pulse as the inlet boundary condition in the SPH model (Figure 4). The blood flow was simulated for 70 cardiac cycles, and pressure in the femoral artery and blood volume was computed. The plots in Figure 4 demonstrate a significant loss in blood volume and a corresponding decrease in pressure. The pressure drop in the simulation was small but would likely increase with more simulated cardiac cycles.

Future work

This work describes iMSTK’s new physiology model via the use of Pulse’s backend. We also report an improved SPH fluid model in iMSTK that allows the simulation of pipe flow. With this model, we were able to demonstrate a potential use case where surgical events (e.g. vessel damage) captured by the high-definition models (SPH-based arterial flow) can be coupled with the 0-D model of the whole-body physiology in real-time. The purview of surgical simulators, typically restricted to the modeling of the surgical corridor, can be extended via such coupling.

In the future, we would like to expose more actions such as airway obstruction, cardiac arrest, substance infusion, and needle decompression commonly observed in the operating room. Incorporation of these actions into the iMSTK-based trainers would allow training for adverse events, ones that often require surgeons and other OR personnel to coordinate mitigation strategies before continuing with the planned surgical procedure. In addition, conditions such as anemia and stenosis will be added to allow users to employ variability in the patients.

Acknowledgments

This work was supported, in part, by the following awards from NIH: 1R01EB025247 and 2R44DK115332.

Disclaimer: The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or its institutes.

References

1. Al-Saad, M., Kulasegaram, S. and Bordas, S. P. A. (2016) ‘Blood flow simulation using smoothed particle hydrodynamics’, Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS Congress 2016).
2. Alvarado-Rodríguez, C. E. et al. (2017) ‘Nonreflecting outlet boundary conditions for incompressible flows using SPH’, Computers & Fluids, pp. 177–188. DOI: 10.1016/j.compfluid.2017.09.020.
3. Monaghan, J. J. (1992) ‘Smoothed particle hydrodynamics’, Annual Review of Astronomy and Astrophysics, pp. 543–574. DOI: 10.1146/annurev.aa.30.090192.002551.
4. Monaghan, J. J. (2012) ‘Smoothed particle hydrodynamics and its diverse applications’, Annual Review of Fluid Mechanics, pp. 323–346. DOI: 10.1146/annurev-fluid-120710-101220.
5. Ozbulut, M., Yildiz, M. and Goren, O. (2014) ‘A numerical investigation into the correction algorithms for SPH method in modeling violent free-surface flows’, International Journal of Mechanical Sciences, pp. 56–65. DOI: 10.1016/j.ijmecsci.2013.11.021.
6. Qin, Y. et al. (2017) ‘Computational evaluation of smoothed particle hydrodynamics for implementing blood flow modeling through CT reconstructed arteries’, Journal of X-ray Science and Technology, 25(2), pp. 213–232.